Introduzione al Teorema di Bayes
Il teorema di Bayes è un principio fondamentale della probabilità che fornisce un modo per aggiornare le nostre credenze sulla base di nuove informazioni. In sostanza, ci permette di calcolare la probabilità di un evento, dato che si è verificato un altro evento correlato.
Il teorema di Bayes trova applicazione in una vasta gamma di campi, dalla medicina alla finanza, dall’intelligenza artificiale alla scienza forense. Per comprendere meglio questo teorema, consideriamo un esempio pratico.
Applicazione del Teorema di Bayes nella Vita Reale
Immaginiamo di voler diagnosticare una malattia rara. Supponiamo che solo l’1% della popolazione sia affetto da questa malattia. Esiste un test per questa malattia che ha un’accuratezza del 90%, ovvero identifica correttamente il 90% dei pazienti affetti e il 90% dei pazienti sani. Se una persona effettua il test e risulta positivo, qual è la probabilità che sia effettivamente malato?
Il teorema di Bayes ci permette di calcolare questa probabilità.
La Formula Matematica del Teorema di Bayes
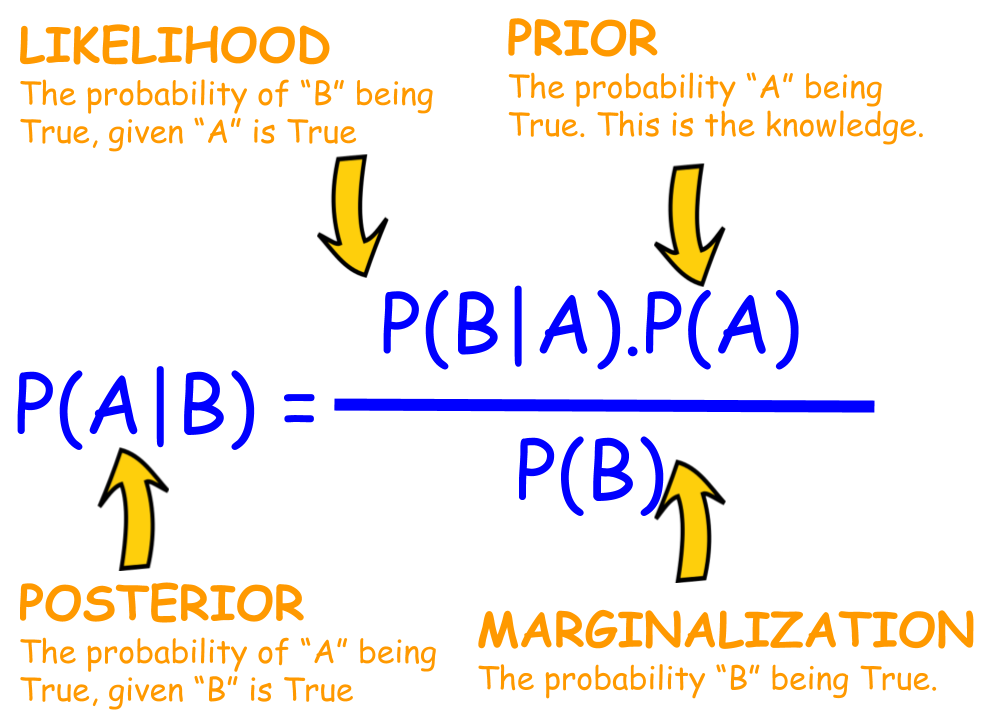
Il teorema di Bayes è espresso dalla seguente formula:
P(A|B) = [P(B|A) * P(A)] / P(B)
Dove:
* P(A|B) è la probabilità dell’evento A dato che si è verificato l’evento B. In questo caso, è la probabilità di essere malato dato che il test è positivo.
* P(B|A) è la probabilità dell’evento B dato che si è verificato l’evento A. In questo caso, è la probabilità di avere un test positivo dato che si è malati.
* P(A) è la probabilità a priori dell’evento A. In questo caso, è la probabilità di essere malati indipendentemente dal test.
* P(B) è la probabilità a priori dell’evento B. In questo caso, è la probabilità di avere un test positivo, indipendentemente dal fatto di essere malati o meno.
Per applicare il teorema di Bayes al nostro esempio, dobbiamo prima calcolare le probabilità a priori. Sappiamo che P(A) = 0,01 (1% della popolazione è malato) e P(B|A) = 0,9 (l’accuratezza del test per i pazienti malati). Per calcolare P(B), dobbiamo considerare la probabilità di avere un test positivo sia per i malati che per i sani:
P(B) = P(B|A) * P(A) + P(B|non A) * P(non A)
Dove:
* P(B|non A) è la probabilità di avere un test positivo dato che si è sani (falso positivo).
* P(non A) è la probabilità di essere sani (1 – P(A)).
Supponendo che P(B|non A) = 0,1 (il test identifica erroneamente il 10% dei sani), possiamo calcolare P(B):
P(B) = (0,9 * 0,01) + (0,1 * 0,99) = 0,108
Ora possiamo applicare il teorema di Bayes per calcolare la probabilità di essere malati dato che il test è positivo:
P(A|B) = (0,9 * 0,01) / 0,108 = 0,083
Quindi, la probabilità di essere effettivamente malati dato che il test è positivo è solo dell’8,3%, nonostante l’accuratezza del test sia del 90%. Questo dimostra che il teorema di Bayes può fornire informazioni preziose per aggiornare le nostre credenze sulla base di nuove informazioni, anche quando queste informazioni non sono perfette.
Applicazioni del Teorema di Bayes

Il teorema di Bayes, come abbiamo visto, fornisce un modo formale per aggiornare le nostre credenze sulla base di nuove informazioni. Questo lo rende uno strumento potente in una varietà di campi, dalla medicina alla finanza, dall’informatica alla scienza dei dati.
Applicazioni del Teorema di Bayes in diversi settori
Il teorema di Bayes trova applicazioni in diversi settori, contribuendo a migliorare la precisione delle previsioni e a prendere decisioni più informate.
| Settore | Applicazione | Esempio | Nota |
|---|---|---|---|
| Medicina | Diagnosticare malattie | Un test per il cancro al seno ha un’accuratezza del 95%. Se il test è positivo, qual è la probabilità che la paziente abbia effettivamente il cancro? | Il teorema di Bayes aiuta a valutare la probabilità di avere una malattia data la positività di un test, tenendo conto della prevalenza della malattia nella popolazione. |
| Finanza | Valutare il rischio di investimento | Un fondo comune di investimento ha una storia di rendimenti elevati. Qual è la probabilità che il fondo continui a generare rendimenti elevati in futuro? | Il teorema di Bayes aiuta a valutare la probabilità di un evento futuro sulla base di informazioni storiche, tenendo conto della volatilità del mercato. |
| Informatica | Filtrare lo spam | Un programma di posta elettronica utilizza il teorema di Bayes per classificare le e-mail come spam o non spam. | Il teorema di Bayes aiuta a classificare le e-mail in base alla probabilità che contengano parole o frasi tipiche dello spam. |
| Scienza dei dati | Analisi dei dati | Un’azienda di e-commerce utilizza il teorema di Bayes per prevedere quali prodotti un cliente è più propenso ad acquistare. | Il teorema di Bayes aiuta a prevedere il comportamento dei clienti in base alle loro interazioni passate con il sito web. |
Aggiornamento delle probabilità
Il teorema di Bayes ci consente di aggiornare le nostre probabilità sulla base di nuove informazioni.
P(A|B) = [P(B|A) * P(A)] / P(B)
dove:
* P(A|B) è la probabilità di A dato che B è vero.
* P(B|A) è la probabilità di B dato che A è vero.
* P(A) è la probabilità a priori di A.
* P(B) è la probabilità a priori di B.
Ad esempio, supponiamo che la probabilità di pioggia sia del 30% (P(pioggia) = 0,3). Se vediamo che le nuvole si stanno addensando (B), possiamo aggiornare la nostra probabilità di pioggia utilizzando il teorema di Bayes. Supponiamo che la probabilità di nuvole dense dato che sta piovendo sia del 80% (P(nuvole dense|pioggia) = 0,8). La probabilità di nuvole dense è del 50% (P(nuvole dense) = 0,5). Utilizzando il teorema di Bayes, possiamo calcolare la probabilità di pioggia dato che vediamo nuvole dense:
P(pioggia|nuvole dense) = [P(nuvole dense|pioggia) * P(pioggia)] / P(nuvole dense) = (0,8 * 0,3) / 0,5 = 0,48
Pertanto, la probabilità di pioggia dato che vediamo nuvole dense è del 48%. Questo dimostra come il teorema di Bayes ci consente di aggiornare le nostre credenze sulla base di nuove informazioni.
Concetti correlati: Bayesian

Il teorema di Bayes è un potente strumento per l’aggiornamento delle nostre convinzioni alla luce di nuove evidenze. Per comprenderlo appieno, è necessario familiarizzare con alcuni concetti chiave, tra cui la probabilità a priori, la probabilità a posteriori e la probabilità condizionata.
Probabilità a priori, a posteriori e condizionata, Bayesian
La probabilità a priori, indicata con P(A), rappresenta la nostra convinzione iniziale sulla probabilità di un evento A prima di osservare qualsiasi dato. La probabilità a posteriori, indicata con P(A|B), rappresenta la nostra convinzione aggiornata sulla probabilità di A dopo aver osservato l’evento B. La probabilità condizionata, indicata con P(B|A), rappresenta la probabilità di B dato che A si è verificato.
Il teorema di Bayes ci fornisce un modo per calcolare la probabilità a posteriori di un evento A, dato che si è verificato un evento B, utilizzando la probabilità a priori di A, la probabilità condizionata di B dato A e la probabilità a priori di B:
P(A|B) = [P(B|A) * P(A)] / P(B)
Inferenza bayesiana
L’inferenza bayesiana è un metodo statistico che utilizza il teorema di Bayes per aggiornare le nostre convinzioni sulla base di nuove evidenze. A differenza dei metodi inferenziali classici, che si basano su ipotesi di probabilità fisse, l’inferenza bayesiana considera la probabilità come una misura della nostra incertezza e la aggiorna man mano che raccogliamo nuovi dati.
L’inferenza bayesiana è particolarmente utile per affrontare problemi con dati limitati o incerti, poiché consente di incorporare le nostre conoscenze a priori nel processo di inferenza.
Esempi di applicazioni del teorema di Bayes
Il teorema di Bayes trova ampia applicazione in diversi campi, tra cui:
* Classificazione: Il teorema di Bayes può essere utilizzato per classificare oggetti o eventi in base a determinate caratteristiche. Ad esempio, un sistema di filtro antispam può utilizzare il teorema di Bayes per identificare e bloccare le email indesiderate.
* Previsione: Il teorema di Bayes può essere utilizzato per prevedere l’occorrenza di un evento futuro, basandosi su dati storici e sulle nostre convinzioni a priori. Ad esempio, un modello di previsione del tempo può utilizzare il teorema di Bayes per prevedere la probabilità di pioggia in base alle condizioni meteorologiche attuali e alle informazioni storiche.
Bayesian analysis, with its focus on updating beliefs based on new evidence, is often used in fields like finance and medicine. It can also be applied to the realm of luxury, such as understanding the market for high-end yachts, like the one owned by Mike Lynch, a prominent figure in the tech industry, a lavish vessel that reflects his success.
By applying Bayesian principles to such data, we can gain insights into the factors that drive demand and price in the luxury yacht market.
Bayesian analysis, a powerful tool for data analysis, often relies on subjective prior beliefs. This is where the personal touch of individuals like Mike Lynch, CEO of Invoke Capital, comes in. His wife, a source of inspiration for him , might unknowingly influence his perspective on certain issues, impacting his Bayesian approach.
Understanding these personal biases is crucial for interpreting and applying the results of any Bayesian analysis.
